Bài 1: Một lớp có 30 học sinh. Cần chọn một bạn làm lớp trưởng, một bạn làm lớp phó và một bạn làm thư ký. Hỏi có bao nhiêu cách chọn, biết rằng học sinh nào cũng có khả năng làm lớp trưởng, lớp phó hoặc thư ký như nhau.
Bài 2: Một lớp có 40 học sinh gồm 25 nam và 15 nữ.
a) Có bao nhiêu cách chọn một học sinh tham gia cuộc thi về môi trường.
b) Có bao nhiêu cách chọn 3 học sinh gồm 2 nam và 1 nữ tham gia sân chơi kiến thức dưới cờ.
c) Có bao nhiêu cách chọn 4 học sinh trực an toàn giao thông, biết rằng trong đó phải có ít nhất 2 học sinh nam.
Bài 3: Một trường phổ thông có 5 học sinh giỏi lớp 10, 6 học sinh giỏi lớp 11 và 8 học sinh giỏi lớp 12. Cần chọn 4 học sinh để tham gia đội tuyển thi “Đố vui để học”. Hỏi có bao nhiêu cách chọn, nếu mỗi khối có ít nhất một học sinh.
Bài 4: Một học sinh có 4 quyển sách Toán khác nhau và 3 quyển sách Văn khác nhau. Cần sắp xếp 7 quyển sách trên thành một dãy theo hàng ngang trên một tủ sách.
a) Hỏi có bao nhiêu cách sắp xếp.
b) Hỏi có bao nhiêu cách sắp xếp nếu 2 quyển kề nhau phải khác nhau.
Bài 5: Từ các chữ số 0,1,2,3,4,5,6,7,8,9 có thể lập được bao nhiêu:
a) Số lẻ có 3 chữ số khác nhau.
b) Số chia hết cho 5 và có 3 chữ số khác nhau.
c) Số chia hết cho 3 và có 3 chữ số khác nhau.
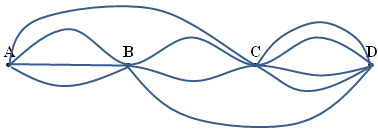
Bài 6: Có bao nhiêu cách đi từ A đến D (mỗi điểm chi được đi qua một lần)